Einstein, Dirac, Wigner, Feynman

  • One hundred years ago, Niels Bohr was worrying about the electron orbit of the hydrogen atom. Albert Einstein was interested in how things appear to moving observers.

  • How would the hydrogen atom look to moving observers? If they discussed this problem, there are no written records on this aspect. Homework problem for younger generations!

  • This is an image of the bridge near Avignon (France) built during the reign of Julius Caesar. This structure is an excellent illustration of what God can do and what humans can to. God created mountains and humans built a bridge.

    To me, Bohr and Einstein are like God-like figures. The best I could do was to build a bridge between them.

  • Then, am I the first one to recognize this problem? The answer is No.

  • Many distinguished physicists worried about this problem. Among them were Dirac, Wigner, and Feynman.
    Let us review their works and integrate them.



Dirac
  1. 1927. c-number time-energy uncertainty relation.
  2. 1945. Harmonic oscillators for the Lorentz group.
  3. 1949. Light-cone coordinate system.
Combine all three. 		Wigner
  1. 1932. Wigner functions.
  2. 1939. Little group for internal space-time symmetries.
  3. 1953. Group contractions.
Combine 1. and 2. Combine 2. and 3. 		Feynman
  1. 1969. Parton model.
  2. 1971. Harmonic oscillators.
  3. 1972. Rest of the universe.
Combine all three.

Major contributions c-number time-energy uncertainty, harmonic oscillators, light-cone coordinate system. Little groups defining internal space-time symmetries. Parton model, oscillator model for Regge trajectories, in addition to Feynman diagrams.


Favorite language Poems. Dirac's writings are like poems. Group theory, and two-by-two matrices. Diagrams and pictures.

Soft spots Lack of figures and illustrations.
Lack of physical examples. Before the age of high-energy accelerators. 		Lack of concrete physical examples. His 1939 paper could not explain Maxwell's equations. He could not explain his parton picure in terms of the mathematical tools developed by Dirac and Wigner.


Mathematical
Instruments

We all know that Einstein's special relativity is best described by a hyperbola, written as
    t2 - z2 = 1.

We can then consider a circle to tangent to this hyperbola and squeeze to produce an ellipse to tangent to the hyperbola. High-school mathematics.

Dirac's idea is to use the Gaussian function (the language of quantum mechanics) for the circle.

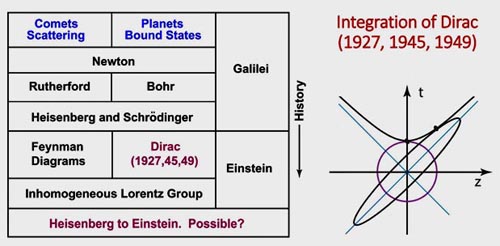
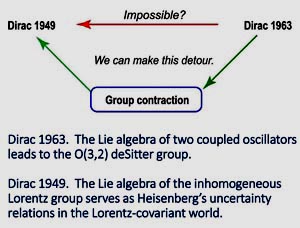
  • Click here for a paper on this subject.

  • Click here for applications of the same mathematics to modern optics.


    • If we integrate those nine papers by Dirac, Wigner, and Feynman, we end up with

    Further Contents of Einstein's E = mc2.


    Einstein's Lorentz-covariant world

    Massive/Slow between Massless/Fast
    Energy Momentum E=p2/2m Einstein's
    E=(m2 + p2)1/2
    		E=p
    Spin,
    Gauge, Helicity     		S3
    S1 S2     		Wigner's
    Little Group     		S3
    Gauge Trans.
    Gell-Mann, Feynman Quark Model Lorentz-covariant
    Oscillators         		Parton Picture
    We can now be more ambitious.
    • Is it possible to derive quantum mechanics (with the Heisenberg brackets) and special relativity (with E = mc2) from one basket of equations? Look at the following papers.

      1. Click here Poincaré Symmetry from Heisenberg’s Uncertainty Relations.

      2. Click here Einstein’s E = mc2 derivable from Heisenberg’s Uncertainty Relations

    • Click here for the recognition I received for my researach efforts.
    • In his paper of 1963, Dirac observed that two coupled oscillators can produce the Lie algebra for the O(3,2) deStter group, namely the Lorentz group applicable to three space coordinates and two time-variables. I met Dirac in 1962,right after he wrote this paper.

    • One of the two time-like variables can be contracted according to the procedure spelled out by Inonu and Wigner in 1953. Thus, the four generators with respect to the second time variable become the translation generators on three space coordinates and time coordinate.

    • The result is the inhomogeneous Lorentz group with three rotations and three boots generators plus four space-time translation generators. This is exactly what Dirac wanted to achieve in his 1949 paper.
    copyright@2021 by Y. S. Kim, unless otherwise specified. The color photo of Dirac by Bulent Atalay, and photo of Wigner by Y. S. Kim (1988). Feynman's photo is from the main lobby of the Feynman Computing Center at the Fermi National Accelerator Laboratory, Batavia, Illinois, USA.