I met Paul A. M. Dirac in 1962.
- When Paul A. M. Dirac visited the University of Maryland in October of 1962, I was a
first-year assistant professor, and I had to provide convenience for him. At that
time, I was confused. The Physical Review Letters was constantly sending out new
words, such as Regge poles, N/D method, bootstrap dynamics, strip approximation, etc.
However, to me, they did not sound like the physics I really wanted to do.
|
I was fortunate enough to spend 30 minutes alone with Dirac. I asked him what
I should do in physics. He said American physicists should spend more time to
understand Lorentz covariance. This was a totally unexpected answer to me.
- It was like the anwer Nicodemus got from Jesus. Nicodemus a Pharisee (upper-class
Jewish man) unhppy with what was happening in his environment and went to Jesus for
wisdom, but he got the anwer totally strange to him.
- It took me some time to understand what Dirac was really telling me.
First of all,
by American physicists, did he meet anyone in particular? It was not until after
reading some of Feynman's papers to realize he was talking about Feynman. Dirac was
right, Feynman or his students could have studied Lorentz transformations more
carefully. For instance, the paper with his students
contains many new physical ideas, but it is a total mess from the mathematical point
of view. They could have done much better job if they had studied Wigner's papers
on the Lorentz group.
Only after I read Feynman's papers, I realized Dirac was talking about Feynman when
he said "American physicists."
Dirac and Feynman met in July of 1962 (three months before I met Dirac). They met
in Poland.
- How about Dirac's papers? The best way to understand what Dirac told me in
1962 was to read Dirac's own papers. Dirac's papers all sound like poems, but they
do not contain figures. The best way to understand his papers is to translate
all those poems into cartoons. Here are thus my cartoons to tell you what Dirac
told me and what I did.
- First of all, let us translate what Dirac told me into a cartoon.
|
|
|

|
|
|
|
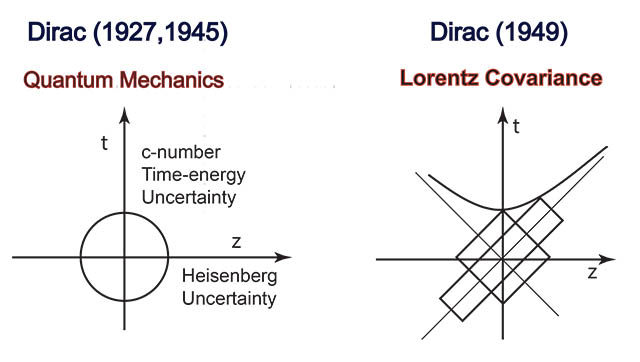
|
|
|
|
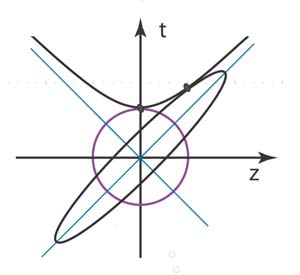
In the real world,
this ellipse appears as
|
|
- You do not have to be a genius to combine the above two figures. This figure
means many different things in physics. Among them are
- Lornerz-covariant picture of bound states.
-
Quarks and partons as one Lorentz-covariant entity.
- Coupled Oscillators as a model for the Lorentz-covariant world.
- Squeezed states of light.
- Squeeze transformations in physics. Symplectic transformations.
- Feynman's rest of the universe.
- Role of entropy in the Lorentz-covariant world.
- Entropy and Lorentz transformations,
Physics Letters A 147, 343 (1990).
- Entangled space and time variables.
- Coupled oscillators, entangled oscillators, and Lorentz-covariant Oscillators
Journal of Optics B:
Qauntum and Semiclassical
7, s 459 - 467 (2005).
ArXiv.

|
I like this computer. It generates both quantum mechanics and
special relativity.
|
- Note added in 2018. After realizing that Dirac's
life-time interest was in making quantum mechanics consistent with relativity,
I became interested what Dirac was really telling me when I met him 1962. In 1962,
he submitted his paper to the Journal of Mathematical Physics, in which he constructed,
from two harmonic oscillators,
the Lie algebra of the Lorentz group applicable to 3-dimensional space with two time
variables.
Click here
for Dirac's 1963 paper.
The harmonic oscillator is the language of quantum mechanics. The Lorentz group is
the language of Einstein's special relativity. Does this mean that the special
relativity is derivable from quantum mechanics? For many years, this has been my
main interest in physics. Click here for my
list of publications.
- Note added in 2019.
I became quite excited about contracting Dirac's O(3,2) group
into the inhomogeneous Lorentz group, and wrote the following three papers.
- Einstein's E = mc^2 derivable from Heisenberg's Uncertainty Relations,
with Sibel Baskal and Marilyn Noz,
Quantum Reports [1] (2), 236 - 251 (2019),
doi:10.3390/quantum1020021.
ArXiv. For pdf with sharper images,
Click here.
- Role of Quantum Optics in Synthesizing Quantum Mechanics and Relativity,
Invited paper presented at the 26th
International Conference on Quantum Optics and Quantum Information
(Minsk, Belarus, May 2019).
ArXiv. For pdf with sharper images,
click here.
- Poincaré Symmetry from Heisenberg's Uncertainty Relations,
with S. Baskal and M. E. Noz,
Symmetry [11](3), 236 - 267 (2019),
doi:10.3390/sym11030409.
ArXiv.
|
|
- The photo of Dirac and Feynman is from the Caltech Photo Archive.
This photo was taken by Marek Holzman during the International
Conference on Relativity Theory of Gravitation in Warsaw (Poland)
on July 25-31 1962, organized by Leopold Infeld. The image of Jesus
and Nicodemus is from "The Picture Bible" (David C. Cook Publishing Co.,
Elgin, Illinois, U.S.A., 1978).
|
|