Photos from the E. Segre Visual Archives of the American Institute of Physics.

• One hundred years ago, Niels Bohr and Albert Einstein met occasionally to discuss physics. Bohr was worrying about the hydrogen atom with its electron orbit. Einstein was interested in how things appear to moving observers.

  It is thus possible that they talked about how the hydrogen would appear to moving observers. If they did, there are no written records on this aspect. The purpose of this webpage is to settle this issue.

• Bohr's worry about the hydrogen atom led to the present form of quantum mechanics based on localized probability distribution. Einstein's concern on moving observers led to his theory of special relativity which leads to his E = mc².

  In this theory, Einstein used the Lorentzian space and time, where the time variable is not separate from the space coordinates for moving obaservers. The mathematics governing this world is called the Lorentz group, and the world to which this mathematics is applicable is the Lorentz-covariant world.

• It was Paul A. M. Dirac (1902-1984) who attempted to formulate the theory of localized probabilty in Einstein's Lorentz-covariant world. He published the following important papers on this subject.

  at the Westminster Abbey (London).

  1. Dirac (1927). The Quantum Theory of the Emission and Absorption of Radiation, Proc. Roy. Soc. (London) A [114], 243 - 265 (1927).

  2. Dirac (1945). The Quantum Theory of the Emission and Absorption of Radiation, Proc. Roy. Soc. (London) A [A183], 284 - 295 (1945).

  3. Dirac (1949). Forms of Relativistic Dynamics, Rev. Mod. Phys. [21] 392 - 399 (1949).

  4. Dirac (1963). A Remarkable Representation of the 3 + 2 deSitter Group, J. Math. Phys. [4], 901 - 909 (1963).

• These four papers are original and deep-penetrating. No ordinary physicists could write papers like these. This does not necessarily mean that there is nothing add to them.
  1. Dirac's papers are like poems. It is a pleasure to read them. However, there are no figures. Thus, we can add figures to his papers.

  2. In his papers, Dirac never mentioned his earlier papers on the same subject. Thus, it is profitable to understand his papers in terms of his earlier thinkings on the same subject.

     Dirac's wife was Wigner's sister. Dirac's time-enery uncertainty added to Heseiber's position-momentum uncertainty.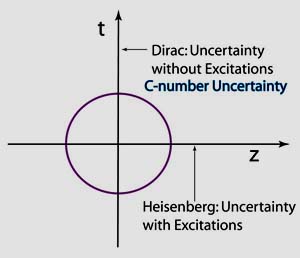

  3. Eugene Paul Wigner (1902-1995) was his brother-in-law. His wife was Wigner's younger sister. In 1939, Wigner published an important paper on internal space-time symmetries of particles in the Lorentz-covarint world. Dirac never made meaningful references to Wigner's 1939 paper. It is thus possible to strengthen is papers using the wisdom contained in Wigner's paper.

• In his paper of 1945, Dirac introduced the time variable in his harmonic oscillator wave functions, but he did not mention the difficulty of incorporating the c-number time-energy uncertainty in the Lorentz-covariant world which he pointed out in his earlier paper of 1927. He could have included this figure in his 1945 paper.

  In his paper of 1945, Dirac was talking about localized waves for bound states using harmonic oscillator wave functions. Dirac did not recognize Wigner's 1939 paper is applicable to the subject.

  For this system, Wignr's little group is O(3), namely the three-dimensional rotation group, for the bound system. This is quite consistent with his c-number nature of the time-energy uncertainty relation which Dirac pointed out in his 1927 paper. Click here for an explanation.

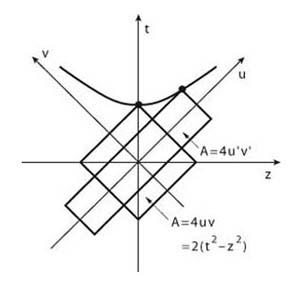
  Dirac's light-cone coordinate system.

• In his 1949 paper, Dirac introduced his light-cone coordinate system.

  Indeed, a very important contribution to Einstein's special relativity!

  However, Dirac did not tell that the Lorentz transformation is an area-preserving squeeze transformation.

  This paper tells that the Lorentz boost is a squeeze transformation, as shown in this figure, resulting in the integration of Dirac's 1927, 1945, and 1949 papers.

• Let us go back to the Bohr-Einstein issue of the moving hydrogen atom. If we translate Dirac's poems into cartoons, they are like the two figures given above. It is then possible to see how the moving hydrogen atom appears to the stationary observer. We can use the following figure to see this effect.

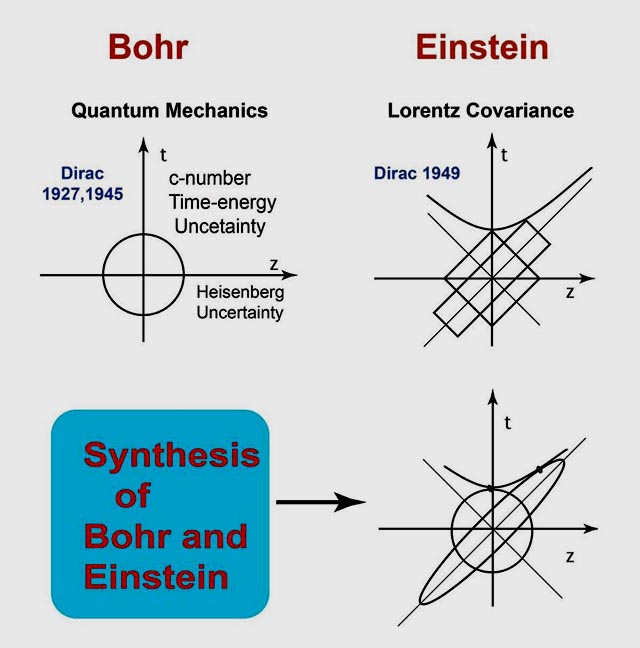
  Integration of Dirac's 1927, 1945, and 1949 papers.

• There comes the most cruel question in physics. Is it possible to see this effect in the real world? It was not possible before 1950. There were no hydrogen atoms moving ast enough to see this elliptic squeeze. However, after 1950, high-energy accelerators started producing protons moving with speed comparable with that of light.

  Click here to enlarge this image.

  Yet, the proton is not a hydrogen atom. What does the proton with ulta-fast speed have to do with the fast-moving hydrogen atom? In 1964, Murray Gell-Mann showed that the proton is a quantum bound state of more fundamental particles called the "quarks." Thus, we can study the quantum mechanics of the hydrogen atom by looking at the proton.

  In 1969, Richard Feynman observed that, when the proton moves with a speed very close to that of light, it appears like a collection of an infinite number of partons.

  Indeed, the following figure shows that Gell-Mann's quark model and Feynman's parton picuture are two different ways of looking at the same Lorentz-covariant entity.

• This figure shows that Gell-Mann's bound state and Feynman's parton picture are two different ways of looking at the same object. My paper publsihed in Review Letters (1989) contains the left half of this figure. Click here for more detailed stories of the Bohr-Einstein and quark-parton issues.
• We have settled the century-old the Bohr-Einstein issue by integrating the papers written by Dirac's in 1927, 1945, and 1949.

Two coupled oscillators lead to ten generators of for the O(3,2) deSitter group, according to Dirac (1963). The four generators involving the second time variable can be converted to the four translation generators along the space and time coordinates.

• In 1963, Paul A. M. Dirac another important paper indicatiing that Einstein's relativistic world could be derived from Heisenberg's uncertainty relations. He only gave an indication, but he did not finish the work. Let us see what he did in his 1963 paper. Then let us finish the task.

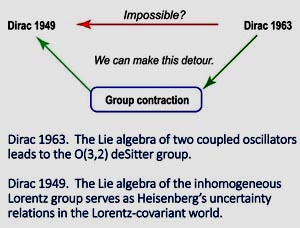
  In his 1963 paper, Dirac constructed the O(3,2) deSitter group from two coupled oscillators. This group is Lorentz group applicable to three space coordinates and two time variables. Compared with the Lorentz group of O(3,1), this group has an extra time variable.

  Earlier in 1949, Dirac said that the task of constructing the quantum mechanics in the Lorentz-covariant world is to construct a representation of the inhomogeneous Lorentz group, consisting of three rotations, three boosts, and four translations.

• Thus, it is fun to see whether it is possible to obtain the inhomogeneous Lorentz group mentioned in his 1949 paper from the O(3,2) group he obtained from two coupled oscillators. Indeed, this is possible. The key is to flatten one of the time variables to make four translation variables, separating O(3,2) into O(3,1) and four translations. This process is called the group contraction introduced by Inonu and Wigner in 1953.

• We thus arrrive at an important conclusion. The special relativity, with Einstein's E = mc², contained in the inhomogeneous Lorentz group is derivable from the Heisenberg brackets. Have you heard this story before? Click here for a published article on this subject.

  We discuss coupled harmonic oscillators in undergraduate physics classes. We never expected this toy could play a role in combining quantum mechanics and special relativity into one scientific discipline. According to philosophers, this is a Hegelian synthesis.

• In 2019, I published the following papers telling that Einstein's E = mc² can be derived from the Heisenberg brackets.
  1. Einstein's E = mc² derivable from Heisenberg's Uncertainty Relations,
     with Sibel Baskal and Marilyn Noz,
     Quantum Reports [1] (2), 236 - 251 (2019),
     doi:10.3390/quantum1020021.
     ArXiv. For pdf with sharper images, click here.

  2. Role of Quantum Optics in Synthesizing Quantum Mechanics and Relativity,
     Invited paper presented at the 26th International Conference on Quantum Optics and Quantum Information (Minsk, Belarus, May 2019).
     ArXiv. For pdf with sharper images, click here.

  3. Poincaré Symmetry from Heisenberg's Uncertainty Relations,
     with S. Baskal and M. E. Noz,
     Symmetry [11](3), 236 - 267 (2019),
     doi:10.3390/sym11030409.
     ArXiv.

• The following figure will illustrate that the progress in physics is made through SYNTHESIS. During the 20th Century, quantum mechanics and relativity were developed, and they were shown to be compatible with each other. The question then is whether they can be synthesized to become ONE THEORY. This question is illustrated in the following table.

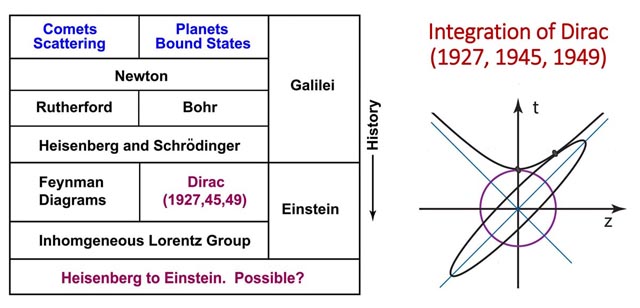
  It is indeed possible to derive Einstein's Lorentz-covariant world from Heisenberg's uncetainty relations.

Click here to enlarge this image.

One hundred years ago, Bohr worried about the minimum radius of the hydrogen atom, leading to the present form of quantum mechanics. Einstein was interested in how things appear to moving observers, leading to his theory of relativity.

God created both Einstein and Bohr. All I can do is to build a bridge between them, by integrating Paul A. M. Dirac's pioneering works.

Acknowledgments

• This webpage is largely based on the paper I published with Sibel Baskal and Mriylyn Noz. Click here for the paper.

• John S. Toll was the Chairman of the Physics Department when I came to the University of Maryland in 1962. He was an ambitious man and invited Paul A. M. Dirac to his department for one week in October of 1962, and he assigned me as the personal assistant to Dirac.

  My photo with Dirac's bust at the Fine Hall Libray of Princeton University (2000).

  I learned valuable lessons directly from Dirac. At that time, he had completed his paper on the O(3,2) group for the two oscillators, which was published in the Journal of Mathematical Physics in 1963. It was three months after he talked with Feynman in Poland (July 1962).

• After a period of stuggles, in 1970, I decided to pursue my own way of doing physics according to what learned from Dirac: to construct quantum mechanics in the Lorentz-covariant world, to synthesize quantum mechanics and relativity, or to settle the Bohr-Einstein issue of moving hydrogen atoms. This webpage started from what I learned from Dirac in 1962.

• copyright@2021 by Y. S. Kim, unless otherwise specified.
  

  How did I talk to Einstein?

• Click here for Y. S. Kim's home page.
  1. Earlier version of this page.
  2. Princeton page.
  3. His Einstein page.
  4. Dirac page.
  5. Wigner page.

  
  I received my PhD degree from Princeton in 1961, seven years after high school graduation in 1954. This means that I did much of the ground work for the degree during my high school years.