 37 (force vectors & motion)
37 (force vectors & motion)
46 (static equilibrium)
53 (stuck car)
58 (spring balances)
61 (scale on skateboard)
72 (blocks & massive rope)
81 (housepainter)
83 (mass & pulleys on ledge) (Answer in book is wrong?!)
98 (wedge & block)
Assignment 14:
due
***Tuesday***, 5/12
reading: relativity supplements
(and Chapter R if you haven't yet
read it)
problems: chapter
R
10 (pion decay, lab frame) (Answers: 49.4 ns, 12.6 m, 6.63 m)
11 (pion decay, pion frame)
33 (energy given velocity)
39 (velocity given energy) (Note: the electron rest energy is 0.511
MeV.)
41 (relativistic vs. non-relativistic kinetic energy)
45 (neutrino mass) Add part (a0) Use problem 39 to show that (since E
>> mc^2), mc^2 =~ E Sqrt[2t/T]. Here =~ means approximately equal,
T is the light travel time, and t is the time delay for the neutrinos. Using
this formula the rest of the problem is simple!

If observer O sends out two pulses of light, separated by a time interval T, another observer O' will receive the pulses separated by another time interval T' which is not equal to T. In fact T' must be proportional to T, as can be seen by a simple argument using the homogeneity of spacetime. Hence T' = k T for some constant k, which characterizes the relative motion of O and O'. Refer to the handout for an introduction to the k-factor. For this problem, let's adopt units with c=1, to simplify the writing. You should insert c in the right places in your final formulas using dimensional analysis.
(a) Draw a spacetime diagram
illustrating the definition of k, showing the worldlines of O and O', the
two light pulses, and the labeled time intervals.
(b) Show that the relative velocity of O and O' is given by v = (k2
- 1)/(k2 + 1). I think this is simplest to see if you assume
that one of the light pulses is sent at the moment the O and O' worldlines
intersect, so that light pulse doesn't even appear on the diagram. Also,
making O's worldline vertical on the diagram probably makes it easier to
see the relations.
(c) Show using (c) that k = Sqrt[(1 + v)/(1 - v)].
(d) Show that if O1, O2, and O3 are
three inertial observers in one dimension, and k12, k23,
and k13 are the k-factors for each of the pairs, then k13
= k12 k23 .
(e) Show using the previous results that v13 = (v 12
+ v23)/(1+ v12 v23). This is the relativistic
velocity addition formula.
(f) Using dimensional analysis, rewrite the above formulae for v, k, and
v13
restoring the implicit factors
of c in the appropriate places.
Assignment 13:
due
***Monday***, 5/5
reading: Chapter R (Relativity)
problems: chapter
11
18 (Hohmann
transfer orbit from Earth to Mars) (Answer: 258 days)
89 (binary
star system)
100 (tides)
supplemental problems:
S1. Show that, for
a body of mass m in a circular gravitational orbit of radius r about a central
mass M >> m,
(a) the kinetic energy
K is proportional to 1/r,
(b) the orbital speed is
proportional to 1/Sqrt[r]
(c) if the zero of potential
energy U is set at r = infinity, then U = - 2K, and E = - K = U/2.
(d) the orbital speed at
radius r is related to the escape speed from radius r by v_escape = Sqrt[2]
v_orbit.
(e) the angular momentum is proportional to Sqrt[r]
S2. Black hole at
the center of the Milky Way: Use the data from the plot of the orbit of the star S2 to estimate the mass
of the black hole using Kepler's third law. (You'll need to get the actual
size of the orbit from the angular size together with the distance to the
galactic center, which is given in the linked article. Note the plane of the orbit is not perpendicular
to the line of sight but the article doesn't tell us in which direction.
Just read off the semimajor axis as if the projected orbit shown were an
ellipse (unless you are really ambitious and want to try to reconstruct the
unprojected orbit from the information given and the local of the black hole
which should be at a focus of the ellipse!))
S3. Lagrange points: A satellite at one of the Lagrange
points will orbit the sun with the same angular speed as the
Earth, staying in a fixed position relative to the Earth. There is currently
a NASA satellite at L2, called MAP (microwave anistropy probe),
which is taking measurements of the cosmic microwave background radiation.
(a) Show that if the angular speed of the satellite's orbit is equal to
that of the earth's orbit, then
F_s/(m_s r) = F_e/(m_e D),
where F_s and F_e are the centripetal forces on the satellite and earth respectively and r and D are the distances from the sun to the satellite and to the earth respectively. (b) Write out this equation explicitly using Newton's law of gravity, but instead of writing your answer in terms of r write it in terms of the distance d = D - r from the earth to the Lagrange point. (c) The resulting equation for d is complicated, but one can get a good approximation for the location of L1 and L2 by keeping only the lowest order term in the ratio x = d/D which will be very small on account of the small ratio of the mass of the earth to the mass of the sun. To access this approximation, replace d by xD everywhere in your equation. Then you can show that by dropping all but the lowest order terms in x, the equation implies x = (M_e/3M_s)^1/3, which is very close to 1/100. Show that your answer for d is thus around four times the distance to the moon. (d) Show that you get the same approximation for x for the Lagrange point L2. (Hint: to get the above approximation you will need to use the fact that (1+x)^n is approximately equal to 1 + nx for nx<<1, so (1 + x)^(-3) is approximately 1 - 3x. In another term you will want to approximate (1 + x)^-1 by just 1, since the rest of that term is already small.)
S4. Gravitational Lensing: Since the gravitational force is proportional to the inertial mass, all masses fall the same way in a gravitational field (the "equivalence principle"). Einstein therefore predicted that light would also fall, and therefore starlight passing nearby the limb of the sun would be deflected. His first calculation of the effect was based on Newtonian physics, and gave the result that the deflection angle is 2GM/bc^2, where G is Newton's constant, M is the mass of the sun, b is the radius of the sun, and c is the speed of light. Later he used general relativity theory for which the result is greater by a factor of two, 4GM/bc^2. In this problem you will derive the Newtonian deflection angle. Consider a particle of mass m and speed v moving in an almost straight line past a mass M, with the distance of closest approach being b. Assuming the deflection is very small, it is given to a good approximation by the angle q = (Dp)/p, where p is the momentum along the direction of motion and Dp is the momentum in the perpendicular direction acquired as a result of the gravitational deflection. Since Dp is to be very small compared to p, we can neglect any equally small change of p (or v) in computing Dp. To compute Dp, observe that it is equal to the net impulse, which is the integral of F_perp dt over all time. Let's take the particle motion to be in the x-direction, and the perpendicular dispacement b of the line of motion from the center of the mass M to be the y-direction. Then dt = dx/v, and the distance from M to m is Sqrt[b^2 + x^2] when m is at the position (x,b). (a) Using these ingredients, show that the deflection angle is given by 2GM/bv^2. (Technical hint: Change variables from x to s=x/b to factor out all the b-dependence from the x-integral!) (b) Put v=c in your answer and evaluate the deflection angle for M the mass of the sun and b the radius of the sun. Multipying by 2, show that you get 1.75 seconds of arc, the angle that Eddington claimed to measure in the famous solar eclipse expedition of 1919, thus supporting Einstein's theory.problems: Chapter 10:
47 (spinning coin)
(Answers: In 10^{-5} SI units: 1.33,1.33,1.33,(8.83, -6.17).)
51 (masses, pulley
& incline via torque) Add part (d) Solve the problem instead
using just energy conservation: express the total mechanical energy
in terms of the height y_1 and velocity v_1 = dy_1/dt of m_1, set
this energy equal to a constant, and take the time derivative of the
resulting equation. You will find an equation for the acceleration a_1
= dv_1/dt. Compare with part (c). (Another way to solve this would be
to get three equations (F=ma for each mass and torque = I alpha for the pulley)
for the three unknowns: the acceleration and the two tensions. This
is less efficient if you don't care to know about the tensions.)
52 (spindown of space capsule) (Hint: At what rate is
angular momentum injected into the gas? (Nozzle velocity is so high
that you can neglect the extra velocity of the gas due to the rotation
of the satellite.)) (Answer: 52.4 s)
56 (putty &
turntable) (Answers: w_i / (1+ mR^2/I_0), w_i (explain
for credit))
67 (thin bar &
blob of putty) (Answers: v_cm = mv/(m+M), w = mMvd/[(ML^2/12)(m+M)
+ Mmd^2].)
68 (thin bar &
hard sphere) (Answer: L Sqrt[(M-m)/12m])
72 (disk &
putty) (Answers:
m v_0 b, 2 m v_0
b/(MR^2 + 2m R^2),
(m v_0 b)^2/(MR^2
+ 2m R^2),1/2 m
v_0^2(1 - 2mb^2/(M+2m)R^2))
78 (precessing
disk) (Answers: 3.27 rad/s, 0.164 m/s, 0.535 m/s^2,
24.5 N, 1.34 N)
82 (conical pendulum)
(Use mass m, length l, and angle theta, rather than numbers.) (Answers: In cartesian coordinates (x,y,z) with
z the vertical direction, the components fo the angular momentum vector
are L
= mvl(cos(theta) cos(wt), cos(theta) sin(wt), sin(theta)), where w
= Sqrt[g/(l cos (theta))] and v = l sin(theta) w. The rest is just calculating dL/dt
and the torque about the point of support and showing that they are equal.)
supplemental problem:
S1. The earth's
axis is tilted at 23.5 degrees away from the normal to the plane of
earths orbit. Lets see how this tilt might be the result of a major collision
with an asteroid. Treat the original earth as a uniform sphere of mass M
and radius R centered at the origin of coordinates and spinning with angular
velocity w about the z axis, counterclockwise looking down on the x-y
plane from positive z. (a) What was the magnitude and direction of the
original earth's angular momentum with respect to the center of the earth?
(b) Suppose a huge asteroid of mass m struck the earth at 70 degrees north
latitude while moving in the x-z plane (y = 0) with velocity +v in the x
direction. What would have been the magnitude and direction of the angular
momentum of the asteroid with respect to the center of the earth? (c) Suppose
that the asteroid speed v was 100 times as great as the original equatorial
speed of the surface of the earth, measured with respect to the center of
the spinning earth. Suppose further that after the impact the mass of the
asteroid spread out, leading to a spherical earth. What must have been the
ratio m/M if the new axis of rotation was tilted at 23.5 degrees to its original
direction? (Hint: Just add the two initial angular momentum vectors
to find the direction of the final angular momentum vector.) (Answers: L = 2/5 MR^2
w zhat, 0.940 mvR yhat, 1/540)
Assignment 11:
problems:
Chapter 9:
102 (billiard ball translation &
spin) (Example 9-14 shows that if h = r + 2/5 r the ball rolls without
slipping from the beginning.) (Answer: 5 v_0(h-r)/2r^2.)
132 (pulled
spool) We demonstrated
this in class. The answer is arccos(r/R). To show this set both
the total force and the total torque to zero.
Chapter 10:
1 (T/F cross product questions)
21 (piano stool) (Explain your answer. Add part (b): if the
kinetic energy changes, where does the energy go to or come from?
22 (tetherball) (Be careful: The pole has finite radius
hence exerts a torque on the ball about the center. See post and puck
discussion on page 323.) (Explain your answer to receive credit.)
35 (cross product practice) (Answer: The book's answer
to part (c) is wrong. It should be -5 khat.)
39 (cross & dot products)
46 (free particle angular momentum & area)
48 (cancellation of torques)
58 (two disks) (Answer: 3/5 w_0.)
59 (string through
hole)
80 (angular momentum & torque on a particle) (Answers: 72t J-s khat, 72 N-m khat t.)
reading: Chapter 10
problems: Chapter 9:
20 (no friction when
rolling without slipping)
28 (spin down of turntable) (Answers: 0.134 rad/s^2,
1.75 rad/s, 7.24 rev)
40 (the "sweet spot" of a uniform rod) (Notes:
(i) "short time" means that you should assume the rod rotates very
little during the time interval Dt, so that F_0 remains approximately
perpendicular to the rod during the interval. (ii) If you've ever played
tennis or used a baseball bat you probably noticed that when you hit the
ball at just thre right spot of th racquet or bat, you feel no recoil on
your hand. This is the "sweet spot". ) (Hints: For part (a), first
find the angular acceleration about the pivot using the torque. Note that
the analog of impulse for rotational motion is the time integral of torque.
For part (b), apply Newton's second law to the tangential acceleration of
the center of mass during the time F_0 is applied.) (Answer: F_0(3x/2L -1))
50 ("The
Beast" baton) (Hint: use the parallel axis theorem for
the spheres.) (Answers: 0.0400 kg-m^2, 0.0415
kg- m^2, ratio 0.964, increase because... )
99 (gears)
(Hint: Apply Newton's second law for angular motion to each
gear to find two equations. The unknowns are the two accelerations, and
the forces the gears exert on each other. However those forces are negatives
of each other, and the two accelerations are related via the known radii
of the gears, so there are only two unknowns.)
113 (stick falling on ice)
122 (perpendicular axis theorem)
127 (pennies on a falling meterstick)
134 (pulled cylinder) (Note: The mass of the "light
drum" can be neglected.)
(Answers: (T/3)(2r/R -1), (2T/3m)(1 + r/R),
r>R/2, same direction as T.)
reading: Chapter 9
problems: Chapter 8:
63 (handball collision with wall)
73 (block & spring collision) (Hint: At the
moment of maximum spring compression the relative velocity of the
two masses is zero.)
86 (Lithium-5 decay) Add part (b) What fraction of the
speed of light are these speeds? (Answers: 1.74 10^7 m/s,
4.34 10^6 m/s.)
95 (cue ball and eight ball)
96 (a particular 2d collision) (Answers:
(v_0/2) i + v_0 j, 1/16 m v_0^2)
102 (collision using cm frame) (Answers: -3 m/s i
, {-2
m/s i, 6 m/s i}, {2 m/s i, -6 m/s i}, {-1 m/s i, -9 m/s i}, 42 J)
118 (same
impulse, different objects) (Answer: 3/4 v i
- v j)
119 (3
to 1 mass ratio and opposite velocities) Solve (b) and (c) of the
problem this way: (i) Assume the basketball of mass 3m is moving with
velocity v and the baseball of mass m is moving with velocity -v. Find
the velocity of the center of mass v_cm. (ii) Find the initial velocities
of the basketball and baseball relative to the center of mass. (iii)
Using the fact that in the center of mass reference frame the velocities
just flip sign, find the final velocities in the reference frame of the
floor. Show that the basketball is at rest and the baseball has velocity
2v. Add a part (d) Check directly that this final configuration has
the same momentum and kinetic energy as the original configuration.
121 (gravitational sling-shot effect)
140 (falling
beads on a balance) (Hint: The average force of
the beads on the pan is the negative of the average force of the
pan on the beads, which is the average rate of change of momentum of
the beads.) (Answer: 31.9 g)
reading: Whatever you haven't yet read of Chapter 8.
problems: Chapter 8:
6
(True/False momentum questions)
28 (railroad car & grain elevator) (Answers:
(a) yes, (b) friction with the falling grain, (c) no...but you must
explain!)
39 (center of mass of a semi-circular half-disk). (You
can use the hoop result (p. 222) or start from scratch, integrating
using polar coordinates.)
52 (3 pieces, initial speed?) (Answer: (c)...but you must explain!)
53 (exploding shell)
54 (gun, bullet, and block on glider) (Answer to
part (c): (m_b/(m_p+m_b)) L.)
55 (object & wedge)
113 (right angle car collision)
127 (rear-end car collision) Add part (b) : Since horizontal friction
acts, horizontal momentum is not conserved (the cars come to rest).
Why is it nevertheless OK to use conservation of momentum to analyze
this collision?
135 (lifting
coiled rope) (The book's answer to part (c) is wrong. The first term should
be Mv^2/L.)
Mars meteorites: "Meteoroid impact is the only natural process capable of launching martian rocks to Earth. To be ejected from Mars a rock must reach the escape velocity of 5.4 km/sec, which is more than five times the muzzle velocity of a hunting rifle. An impact capable of ejecting the martian meteorites into space would have left a crater of 10-100 km. The meteorites spent several million years in space before landing at various sites on Earth." For a more comprehensive site see http://www.jpl.nasa.gov/snc/
reading: Chapter 7
problems:
Chapter 5:
118 (block sliding off sphere) Add part (0):
Using dimensional analysis, first show that the angle at which
the block leaves the sphere is independent of its mass, the radius
of the sphere, and the acceleration of gravity. (Hint: when
the block leaves the sphere the normal force is zero.)
(Answer: arccos(2/3))
Chapter
6:
22 (raising a box) Add part (d) What is the final
speed of the box? (Answers: 240J, -177 J, 63.0J, 4.60
m/s)
25 (work from a graph)
34 (two pulleys) (Answers: 2h, wh, wh, 2)
39 (force and displacement with vector components)
45 (circular motion another way)
56 (Victoria falls) (Answer: 879 MW)
57 (box sliding down incline)
72 (lifting the country) (Answer: 323 km)
80 (work of non-constant force along different paths) (Answers: 0, 78.0 J)
82 (work and power for a non-constant force) (Answers: 9.00 J, -22.1 W)
87 (work of a tangential force)
88 (work of a centripetal force)
(Answers: -0.9 J, 0,
0.463 m/s)
supplemental problem:
S1.
In class we loaded a bow string and saw that for 1, 2, 6, 7,
11, 12 kg the corresponding stretches were roughly 3, 7, 24.75,
29, 42,5, 45 cm respectively. Newton's third law tells us that
the force exerted by the bow in these configurations is equal to the
weights of these masses. (a) Make a plot of force vs. stretch x
for this data using Excel or a graphing calculator or by hand, and fit
to a straight line |F| = kx + b. (In Excel, make a scatter plot
and use "Add trendline..." under the chart pulldown menu. Choose linear
type and under options check "Display equation".) The data fit a straight
line quite well. (The intercept b will be close to zero.) Evaluate the
spring constant k. (b) Using your value of k compute the work done in stretching
the bow to 40 cm. (I found 20.1 J.) (c) The mass of the arrow was 30
gm. Find its launch speed.
reading: Chapter 6
problems: Chapter 5:
14
(racetrack: force on passenger)
16 (loop-the-loop)
19 (terminal speed)
27 (stopping distance)
42 (Lou's bet)
48 (minimum force)
53 (stacked blocks)
71 (two rotating blocks)
73 (swinging child)
91 (max and min speed on banked curve)
109 (upside down carnival ride)
112 (Babylon 5)
reading: Chapter 5
problems: Chapter 4:
 37 (force vectors & motion)
37 (force vectors & motion)
46 (static equilibrium)
53 (stuck car)
58 (spring balances)
61
(scale on skateboard)
72
(blocks & massive rope)
81 (housepainter)
83 (mass & pulleys on ledge) (Answer in
book is wrong?!)
98 (wedge & block)
Supplemental problems:
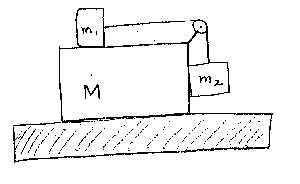
S1. What horizontal force
F must be constantly applied to M so that m1 and m2 do not
move relative to M? Neglect friction. (The table in the figure
is supposed to be horizontal.)
S2. In
class we fired a pencil part way through a piece of plywood.
The pencil had a mass of 4.5 grams, was travelling at 300
m/s, and came to rest after travelling about 7 cm. (a) What
force, assumed constant, acted on the pencil to bring it to rest?
(b) How long did it take for the pencil to stop moving? (c) The pencil
was accelerated by a blast of CO2 through a tube. If the tube was 70
cm long what force, assumed constant, acted on the pencil to accelerate
it to 300 m/s? (Use your result from part (a). Do not recalculate from
scratch!)
S3. An asteroid is discovered to be on a collision course with the earth, and some physics students are desperately trying to devise a way to avoid this calamity. The asteroid has a mass m and is traveling at a speed v toward the collision point, which is at a distance d from the present location of the asteroid. Ignoring gravity, the students determine what constant force F, applied perpendicular to the initial direction of motion during the entire path, is required to deflect the asteroid by one earth radius R by the time it reaches the vicinity of the earth. (a) Using dimensional analysis and the limiting cases of large d or large R, guess their answer up to a numerical constant. (b) What is their result? (Hint: Since the deflection is so tiny, it is very accurate to assume the asteroid travel time is just d/v.) (c) Assuming the asteroid is a sphere of radius 1 km, has a density equal to the average density of the earth, is located at a distance d equal to six times the radius of earth's orbit around the sun, and has a speed v equal to the earth's orbital speed, what is F in Newtons? (You can find the relevant numbers in the textbook on the inside front cover or in Appendix B.)
Assignment 3:
due Friday, 2/14
reading: Chapter 4,
Chapter 5-1
problems:
Chapter 3:
11 (velocity and acceleration vectors)
27 (relative velocity vector)
29 (path, velocity, acceleration)
48 (vector magnitude and direction practice)
64 (swimming across the current)
72 (centrifuge)
109 (aiming a bullet) (This should
be a one or two "dot" problem.) (Note: since the angle of aiming
above the horizontal is going to be very small, you can and should
use the small angle approximation for the sin function, sin x =~
x.)
110 (vector practice)
114 (hammer off roof)
116 (constant acceleration)
Supplemental problems:
I use boldface
for vectors, Ahat for A with a hat over it, D for
what is usually the Greek letter Delta, w for what is usally the
Greek letter omega. Watch out for similar html accomodations
as we go along. (I may be able to insert the Greek fonts later.)
S1. For any vector A we can define a unit vector in the direction of A by Ahat = A/|A|. If A = 3 i + 4 j, what is Ahat?
S2. Consider a particle moving with constant speed in a circle of radius r centered on the origin in the x-y plane. (a) Carefully draw a diagram showing the circular path of the particle. Use a protractor or a drinking glass or something else so your circle is circular. (b) Use a ruler to carefully draw two position vectors r(t) and r(t+Dt) on your diagram, one at some particular time t and one at t+Dt. Label these and all vectors in this problem. Assume the particle goes around 1/32 of the circle in the time Dt. (c) Draw the displacement vector Dr between these two times. (d) On the same diagram draw vectors showing the velocity v at t and t+Dt. (e) Draw the change Dv in the velocity vector between these two times. Locate the tail of Dv at the tip of v(t). (f) On the same diagram draw the acceleration vector a(t). (g) Draw a new diagram showing the circular path, this time including only the three vectors r(t), v(t), and a(t).
S3. Now let's treat the previous
problem using calculus. The position vector is r(t)
= (r cos wt) i + (r sin wt) j, where w is called
the angular velocity. (a) What are the dimensions of w? (b) What
is the relation between w and the period T of one cycle around the
circle? (c) What is the velocity vector? (d) What is the magnitude
of the velocity vector, i.e. the speed v? (e) What is the acceleration
vector? Show that it is proportional to the position vector. (f) What
is the magnitude of the acceleration vector? Express your answer in
two different ways: (i) in terms of r and the angular speed w,
and (ii) in terms of r and the tangential speed v. (g) Evaluate
the position, velocity, and acceleration vectors at the times when wt
= 0, Pi/4, Pi/2. Draw a diagram like in the previous problem showing
all three vectors at these three times, and compare with part (g) of
the previous problem.
reading: Chapter 3
problems: (problems,
answers part 1,
part 2)
chapter 2:
67 (instantaneous velocity from limit)
76 (landslide)
78 (loose elevator bolt)
88 (flower pot & window)
91 (school zone)
107 (catch up with train)
116 (graphical integration)
118 (differentiation & integration)
122 (non-constant acceleration)
optional
challenge: 128 (acceleration
as a function of position)
reading: Chapters 1 & 2
problems:
(scanned pages: page 1, page 2, answers)
chapter 1:
18 (prefixes)
21 (SI units)
24 (unit conversion)
34 (dimensions)
37 (dimensional analysis)
44 (prefixes & scientific notation)
46 (significant figures & scientific notation)
56 c,d only (follow instructions of prob. 46)