Helping physics students learn how to learn
Andrew Elby
Dept. of Physics, University of Maryland
College Park, MD 20742-4111
Abstract:
Students' “epistemological” beliefs—their views about the nature of knowledge and learning—affect how they approach physics courses. For instance, a student who believes physics knowledge to consist primarily of disconnected facts and formulas will study differently from a student who views physics as an interconnected web of concepts. Unfortunately, previous studies show that physics courses, even ones that help students learn concepts particularly well, generally do not lead to significant changes in students' epistemological beliefs. This paper discusses instructional practices and curricular elements, suitable for both college and high school, that helped students develop substantially more sophisticated beliefs about knowledge and learning, as measured by the Maryland Physics Expectations Survey (MPEX) and by the Epistemological Beliefs Assessment for Physical Science.
Building upon the line of inquiry initiated in this journal by Redish, Saul, and Steinberg, [1] I discuss how teachers can help to bring about changes in students' epistemological beliefs—their views about what it means to learn and understand physics. As Hammer [2] shows, some students view physics as weakly connected pieces of information to be separately learned, whereas others view physics as a coherent web of ideas to be tied together. Some students equate learning physics with retaining formulas and problem-solving algorithms, while others think that learning involves relating fundamental concepts to problem-solving techniques. Some students believe learning consists primarily of absorbing information, while others view learning as building one's own understanding.
Epistemological sophistication is valuable. Previous studies show that students' epistemological expertise correlates with academic performance and conceptual understanding in math and science. [3] These correlations exist even controlling for confounding factors such as interest in science, mathematical aptitude, and socioeconomic status. [4] So, we can reasonably infer that a sophisticated epistemological stance supports productive study habits and metacognitive practices. For instance, a student who sees physics knowledge as a coherent web of ideas has reason to “switch on” the metacognitive practice of monitoring one's understanding for consistency. [5] In addition, helping students to understand the importance of consistency and coherence, and the difference between rote memorization and deeper understanding, is arguably a worthy instructional goal in its own right. After all, it's important that students can solve conservation of momentum problems; but in the long run, it's equally important that their beliefs about knowledge and learning engender a sophisticated approach to (re)learning that kind of material. Perhaps, to best prepare students for advanced work in science, engineering, and medicine, instructors of introductory physics courses should focus more on epistemological development and less on content coverage.
Of course, this proposal deserves no attention if physics classes inevitably fail to help students develop epistemologically. Previous research isn't encouraging: Many of the best research-based reformed physics curricula, ones that help students obtain a measurably deeper conceptual understanding, generally fail to spur significant epistemological development.1 Apparently, students can participate in activities that help them learn more effectively without reflecting upon, and changing their beliefs about, how to learn effectively. These students may revert to their old learning strategies in subsequent courses.
In this paper, I show that instructional practices and curricular elements explicitly intended to foster epistemological development can lead to significant improvement in students' views about knowledge and learning. An honors-level curriculum taught to gifted students at a magnet high school in Virginia, and perhaps more significantly, a non-honors physics curriculum taught at a comprehensive high school in California, produced significant pre-post gains in students' scores on the Maryland Physics Expectations Survey (MPEX) and on the Epistemological Beliefs Assessment for Physical Science (EBAPS), a similar assessment developed for high school (rather than college-level) physics students. Although different in many respects, both courses contained common elements discussed in section 4. Most of these elements are suitable for both high school and college.
After describing in section 2 how I “measured” my students' epistemological beliefs, I present the major results in section 3. Then, in section 4, I describe elements of the curricula, acknowledging the trade-offs associated with a strong focus on epistemological development.
California. During the 1997-98 academic year, the subjects were my physics students at a small, comprehensive high school serving a middle-class community in the San Francisco Bay area. The 30-member class consisted of 12th, 11th, and 10th graders. 43% were female. Because the school offers only one physics class besides Advanced Placement, the class was diverse in terms of interest and ability. [6] I had nearly complete control over the curriculum. Due to absences and shuffling class schedules, n = 27 students completed the pre- and post-assessment described below.
Virginia. During the 1998-99 academic year, the subjects were my 76 physics students at a large magnet high school for gifted and talented students near Washington D.C. 50% of my students were female. Since the school requires all 11th graders to take Physics, I was one of five physics teachers. A State-mandated curriculum required me to cover large numbers of topics. This core curriculum was “enforced” by shared, department-wide midterm and final exams. (In Section 4, I will discuss how these exams influenced, and were influenced by, my actions.) Due to extensive shuffling of class schedules at the beginning of the year, n = 55 students took the pre- and post-assessments.
I used two independently-developed epistemological assessments. The Maryland Physics Expectations Survey (MPEX) developed by Redish, Saul, and Steinberg1 and aimed at students taking college-level physics, probes students' beliefs by posing statements, such as
Students choose “strongly agree, agree, neutral, disagree, or strongly disagree.” The above item probes whether students view learning in their physics class as absorbing information or as constructing their own understanding (Independence of Learning); and whether they view mathematical equations as disconnected problem-solving tools or as expressions of conceptual content (Math integration). The italics denote MPEX subscales. Since physics experts tend to disagree with the statement, disagreement or strong disagreement gets scored as “favorable,” while agreement or strong agreement counts as “unfavorable.”
MPEX items also explore whether students view physics knowledge as a collection of pieces or as a more integrated whole (Coherence); whether they view physics as consisting more of formulas and facts or of concepts (Concepts); the extent to which they view physics as connected to their lives outside the classroom (Reality Link); and the extent to which certain varieties of sustained effort lead to success in physics class (Effort). [7]
I also used the Epistemological Beliefs Assessment for Physical Science (EBAPS), developed by a team at the University of California, Berkeley. [8] It differs from MPEX in four ways. First, it targets high-school-level chemistry, physics, and physical science classes, which often involve less math than college-level classes do. Second, as described in Section 3.3, EBAPS subscales differ slightly from MPEX subscales. Third, in addition to MPEX-style agree/disagree items, EBAPS poses multiple-choice questions, as well as mini-debates. An example:
Brandon: A good science textbook should show how the material in one chapter relates to the material in other chapters. It shouldn't treat each topic as a separate “unit,” because they're not really separate.
Jamal: But most of the time, each chapter is about a different topic, and those different topics don't always have much to do with each other. The textbook should keep everything separate, instead of blending it all together.
With whom do you agree? Read all the choices before circling one.
(a) I agree almost entirely with Brandon.
(b) Although I agree more with Brandon, I think Jamal makes some good points.
(c) I agree (or disagree) equally with Jamal and Brandon.
(d) Although I agree more with Jamal, I think Brandon makes some good points.
(e) I agree almost entirely with Jamal.
Response (b), like response (a), gets tallied as “sophisticated,” since Jamal makes the good point that a textbook can easily become overwhelming by immediately diving into the deep, subtle connections between ideas that are still new and confusing to the student.
The fourth way in which EBAPS differs from MPEX is more subtle. By construction, MPEX probes a combination of students' epistemological beliefs about knowledge and students' expectations about their physics course. For instance, consider this MPEX item:
If a student thinks that understanding physics means knowing definitions and algorithms, then her agreement with this item reflects her epistemological orientation. However, in a fast-paced course that rewards the quick, rote application of algorithms, a student may ruefully agree with the statement even though she knows that understanding physics involves insight and creativity. In this case, the agreement stems not from her epistemological outlook, but rather, from her expectations about the exams in a particular class. Again, Redish et al. designed MPEX to probe both epistemology and expectations. By contrast, EBAPS was constructed to probe epistemology alone, to the extent that it can be teased apart from expectations. See www2.physics.umd.edu/~elby/EBAPS/home.htm for the entire assessment, and for more discussion of these issues.
In Virginia (1998-99), on the first day of class (September) and during the last week of class (June), MPEX and EBAPS were given as an “opinion survey” homework assignment, with students receiving full credit for handing it in. In California (1997-98), I administered EBAPS as a pre- and post-test in the same way. The California students did not take MPEX, which is optimized for college-level mathematical physics courses. Since the Virginia students took both assessments, however, it's possible to “cross-calibrate” the two surveys. By June, in both Virginia and California, students had received full credit on numerous “opinion” homework assignments whether or not their views agreed with mine. In addition, their answers to opinion questions throughout the year indicated most students' willingness to disagree with the teacher.
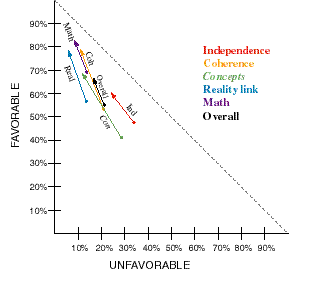
To obtain matched pre-post data, I include only those students who took MPEX as both a pre- and a post-assessment. Following Redish et al.,1 I present the results by specifying the percentage of favorable vs. unfavorable responses to items in each subscale. For instance, in Table 1, the “pre, Coherence” cell in Table 1 indicates that, in September, 53% of students' responses to items in the Coherence cluster (subscale) were favorable, while 21% were unfavorable. Since students sometimes chose “neutral” instead of “agree” or “disagree,” these percentages sum to less than 100%. Figure 1 represents the same data in an agree-disagree plot. For every cluster, a matched (paired) samples t-tests reveals the pre-post changes in the percentage of favorable responses to be statistically significant to p < .01.
| Overall | Independ. | Coherence | Concepts | Reality link | Math | Effort | |
| Pre | 55/21 | 49/34 | 53/21 | 41/28 | 57/13 | 68/16 | 74/11 |
| Post | 66/17 | 60/24 | 78/11 | 68/12 | 78/6 | 82/8 | 55/28 |
| Mean gain
score |
11** | 11* | 25** | 27** | 21** | 14* | –18** |
| S.D. of gain scores | 20 | 28 | 32 | 32 | 36 | 33 | 29 |
TABLE 1: Virginia MPEX scores. The first two rows show the pre and post percentage of favorable/unfavorable responses for each cluster. Each student's gain score is the difference between her percentage of favorable responses on the pre- and post-tests. The fourth row shows the standard deviation of the gain scores, which is relevant for the paired (matched) samples t-test of statistical significance.

FIGURE 1: Agree-disagree plot for Virginia MPEX results. For each MPEX cluster, the base of the arrow represents the pre-test favorable and unfavorable percentages, while the tip of the arrowhead represents the post-test percentages. “Coh” stands for Coherence. This plot omits the Effort cluster, on which the students showed a substantial decline; see Table 1.
Redish et al.1 found that students' overall MPEX scores do not improve significantly between the beginning and end of the course, even at colleges and universities employing research-based, reform-oriented curricular elements such as the University of Washington tutorials, [9] the University of Minnesota context-rich problems, [10] and Dickinson College Workshop Physics. [11] These active-learning curricula all lead to significantly better conceptual learning than traditional curricula do, as measured by the Force Concept Inventory and other assessments. [12] Therefore, Redish et al's MPEX results suggest that students can engage in productive learning without reflecting upon, and changing their beliefs about, the nature of knowledge and learning. I will return to this point in Section 4.
To put my MPEX results in context, it is helpful to review the best MPEX results from Redish et al.'s study. In Dickinson College's Workshop Physics, students spend no time in lecture and essentially all their time interactively engaging with the material and with each other. In that class, the percentage of favorable responses increased slightly for the cognitive subscales inspired by Hammer's work—5% for Independence; 8% for Coherence; and 11% for Concepts, with no changes in the rate of unfavorable responses. The other subscale scores showed no change or a deterioration, leading to no change in the Overall MPEX score. I take these results to show that even the best learning environments do not automatically lead students to rethink their epistemological outlook.
The substantial deterioration in my students' beliefs and expectations about Effort was typical of the colleges and universities studied by Redish et al.
Of course, since the Virginia magnet-school students have unusually high ability and motivation, these MPEX results on their own do not indicate the effectiveness of my curriculum. In the next section, however, I present evidence that my (non-honors) California students underwent just as much epistemological change as my Virginia students.
A reader could also argue that the MPEX gains stem from the efforts of a particular instructor, not from widely-implementable curricular elements. Section 4.8 addresses this issue.
The first three EBAPS subscales roughly correspond to MPEX subscales, as shown in italics on Tables 2 and 3. [13] EBAPS subscale 4, Tentativeness, probes the epistemological sophistication that students bring to the task of sorting out which scientific knowledge is more tentative vs. more “settled.” Subscale 5, Source of ability to learn, gets at the following issue: Is success at learning and doing science almost entirely a matter of fixed natural ability? Or, can people become better at learning and doing science through hard work and appropriate strategies?
A student's response to each EBAPS item receives a score of 0 to 100, with 0 = very unfavorable, 50 = neutral, and 100 = very favorable. Averaging the scores for each item in a cluster gives the corresponding subscale score. These numbers are not percentages of favorable or unfavorable responses; the multiple question types used in EBAPS do not invite this representation of the data.
As Table 2 shows, the Virginia students' EBAPS results correspond closely to their MPEX results, with the largest gain in the subscale corresponding to Coherence and Concepts, and smaller but significant gains in the subscales corresponding to Independence and Reality link. Table 3 shows that, as compared to the Virginia students, the California students achieved essentially identical gains in the cognitive subscales, but not in Real-life applicability. Indeed, this failure in California (1997-98) caused me to use more real-life examples and to make other modifications when I taught in Virginia (1998-99).
VIRGINIA
| Overall | Structure of knowledge
Concepts, Coh. |
Nature of learning
Independence |
Real-life applicability
Reality link |
Evolving knowledge | Source of ability... | |
| Pre | 67.4 | 67.9 | 66.8 | 72.4 | 67.0 | 67.4 |
| Post | 71.8 | 76.1 | 72.7 | 77.1 | 69.5 | 66.3 |
| Mean gain
score |
4.4* | 8.2* | 5.9* | 4.7* | 2.5 | –1.1 |
| S.D. of gain scores | 7.5 | 16.2 | 12.3 | 14.5 | 18.3 | 16.1 |
TABLE 2: Virginia EBAPS scores. The first two rows show the mean pre and post scores for each subscale. “Source of Ability...” stands for Source of Ability to Learn. Keep in mind that that these scores are not percentages of favorable responses, and therefore cannot be compared directly to MPEX scores. Each student's gain score is the difference between her pre- and post-test score. The fourth row shows the standard deviation of the gain scores, which is relevant for the paired (matched) samples t-test of statistical significance.
CALIFORNIA
| Overall | Structure of knowledge
Concepts, Coh. |
Nature of learning
Independence |
Real-life applicability
Reality link |
Evolving knowledge | Source of ability... | |
| Pre | 66.5 | 62.5 | 68.4 | 73.0 | 63.9 | 72.6 |
| Post | 71.8 | 70.9 | 75.0 | 73.5 | 67.9 | 77.4 |
| Mean gain
score |
5.3* | 8.4* | 6.6* | 0.5 | 4.0 | 4.8 |
| S.D. of gain scores | 8.7 | 17.7 | 11.9 | 115.6 | 21.5 | 17.3 |
TABLE 3: California EBAPS scores. See the caption to Table 2 for explanation. On most subscales, the average California gain was greater than the average Virginia gain, though not by a statistically significant margin.
In both California and Virginia, my curricula failed to change students' beliefs about Source of Ability to Learn, despite my efforts.
I did not design my curricula to foster development along the Evolving knowledge subscale. This decision stemmed partly from personal preference, and partly from the following fact: In introductory physical science and math, where the target knowledge is comparatively settled, a sophisticated approach to sorting out which knowledge is more tentative and which knowledge is more settled does not necessarily help students learn the material more effectively, as Schommer et al. show. [14] My own work confirms this conclusion. For my California students, the correlation coefficient between their score on a midyear exam covering Newtonian mechanics and their EBAPS Nature of Learning subscale score was 0.56. For Structure of knowledge, the correlation was .41, also statistically significant (p < .05). But there was essentially no correlation (r = .01) between the exam score and Tentativeness subscale score. (For the Virginia students, EBAPS scores didn't correlate with midyear exam scores, possibly because the tiny standard deviation in students' exam scores, only 4%, allowed non-epistemological factors to wash out any correlations.)
In California (1997-98) and Virginia (1998-99), I taught two different curricula to two different sets of students—a non-honors, slower-paced course vs. an honors, faster-paced course. Both curricula contained common elements discussed in the next section. The California and Virginia students achieved significant—and according to EBAPS, comparable—gains in the sophistication of their beliefs about the coherence and “conceptual-ness” of physics knowledge and about the constructive nature of learning, showing that an epistemology-focused course can work for both average and talented students. In addition, the Virginia students also acquired more favorable beliefs about the link between physics and real life outside the classroom, and about the meaningfulness of mathematical equations. These results came at the expense of content coverage, but not at the expense of basic conceptual development. [15] By contrast, even the best curricula aimed at conceptual development but not aimed explicitly at epistemological development do not produce comparable epistemological results.
In this section, I present some elements of my curricula. High school and college instructors, even ones teaching large lecture classes, could mold these elements to suit their own needs, assuming students spend much of their time in lab and/or discussion sections. I also highlight the trade-offs associated with certain elements. My discussion does not focus on elements that resemble other reform curriculum. However, I want to acknowledge that much of what I do is based on Workshop Physics,11 RealTime Physics labs, [16] the University of Washington tutorials,9 and Mazur's conceptual questions. [17]
I should clarify two points before diving into the details. First, I present these ideas as illustrations of epistemology-focused instruction, not as pre-packaged materials. Labs, grading policies, and other elements must be adapted to the level and motivation of the students, the class size, the instructor's preferences, the flow of the class, and other factors. For instance, I used different Newton's law labs with my Virginia and California students, though I lack the space here to show both versions. Second, as discussed in more detail below, shoehorning a couple of these elements into an otherwise-unchanged class may accomplish little. Preliminary evidence suggests that a focus on epistemology needs to suffuse the class in order to have a significant effect.
I used labs and other materials explicitly designed to integrate conceptual development with epistemological development. In this subsection, I describe two force labs designed to help students understand that learning physical laws involves refining one's intuitive ideas in order to reconcile them with the physics. In other words, these materials try to push students towards Einstein's view that science is “the refinement of everyday thinking.” [18] By contrast, many students initially view common sense as a “separate” kind of thinking that can't be trusted in physics class; see Hammer. [19]
Newton's 2nd law lab.
My first force lab begins in the style of some University of Washington tutorials,9 eliciting and confronting a common student difficulty:
1. A car cruises steadily down the highway at 60 mph. Wind resistance opposes the car's motion with a force of 5000 newtons. Intuitively is the forward force on he car less than 5000 newtons, equal to 5000 newtons, or greater than 5000 newtons? Explain.
2. In this question, we'll see if Newton's 2nd law agrees with your intuitive guess.
(a) When the car cruises at constant speed 60 mph, what is its acceleration, a? Explain your answer in one sentence.
(b) Therefore, according to Fnet = ma, when the car moves at constant velocity, what net force does it feel?
(c) So, is the forward force greater than, less than, or equal to the 5000 newton backward force? Does this agree with your intuitive answer to question 1?
The next question, however, asks students to reflect on the corresponding epistemological issue:
3. Most people have—or can at least understand—the intuition that the forward force must “beat” the backward force, or else the car wouldn't move. But as we just saw, when the car cruises at steady velocity, Newton's 2nd law says that the forward force merely equals the backward force; Fnet = 0. Which of the following choices best expresses your sense about what's going on here?
(a) Fnet = ma doesn't always apply, especially when there's no acceleration.
(b) Fnet = ma applies here. Although common sense usually agrees with physics formulas, Fnet = ma is kind of an exception.
(c) Fnet = ma applies here, and disagrees with common sense. But we shouldn't expect formulas to agree with common sense.
(d) Fnet = ma applies here, and appears to disagree with common sense. But there's probably a way to reconcile that equation with intuitive thinking, though we haven't yet seen how.
(e) Fnet = ma applies here. It agrees with common sense in some respects but not in other respects.
Explain your view in a few sentences.
In California, no single answer got a majority, and the most popular were (b), (c), and (d). In Virginia, most students chose (d) or (e). The rest of the lab was designed not only to help students understand Newton's 2nd law, but also to help them realize that a large part of “understanding” a physical law is reconciling it, to the extent possible, with common sense. In California, students began by pulling a cart across the carpet with a rubber band. They were asked to focus on the following issue:
4. Is there a difference between how hard you must pull to get the cart moving, as compared to how hard you must pull to keep the cart moving? You can answer this question by “feeling” how hard you're pulling, and by observing how far the rubber band is stretched.
Students could see and feel that more force was needed to initiate than to maintain the motion. In the tutorial-style follow-up questions, students related their experimental observations to Newton's 2nd law:
5. Let's relate these conclusions to Newton's 2nd law.
(a) While you get the cart moving (i.e., while it speeds up from rest), does the cart have an acceleration? So, according to Newton's 2nd law, does the forward force beat the backward force or merely equal the backward force? Explain.
(b) While you keep the cart moving (at steady speed), does the cart have an acceleration? So, according to Newton's 2nd law, does the forward force beat the backward force or merely equal the backward force?
(c) Look at your answers to parts (a) and (b). Using Newton's 2nd law, explain why experiment 4 came out the way it did. Check your answer with me.
Question 6 then asked students about the force needed to get the cart moving vs. to keep it moving in the absence of friction. Finally, students were asked to summarize the main conceptual point of the lab:
7. OK, here's the punch line. Most people have the intuition that, if an object is moving forward, there must be a (net) forward force. Explain in what sense that intuition is helpful and correct, and in what sense that intuition might seem misleading.
As often happens in labs, some students needed help “seeing what they're supposed to see” (or in this case, “feeling what they're supposed to feel”) in the experiment. Except for that difficulty, almost all students in both Virginia and California worked through questions 1-6 with minimal help from the teacher. (Before the lab, the California students worked through a few examples designed to illustrate what the “net” force means.) About a third of the California students, and a smaller fraction of the Virginia students, had trouble tying it all together in question 7, though most students responded that the “motion requires force” intuition applies to getting an object moving but not to keeping it moving. Still, especially in California, a post-lab class discussion was needed to help everyone get this point. The class discussion also aimed to help students tie together the main epistemological point of the lab, that learning physical laws is partly a matter of refining rather than abandoning your intuitive ideas.
Newton's 3rd law lab.
My Newton's 3rd law lab continues to push students toward Einstein's viewpoint. Once again, the beginning of the lab resembles a tutorial9 or a RealTime physics lab:16

FIGURE 2: Moving truck rams into parked car, from the Newton's 3rd law lab. Which vehicle feels a bigger force from the other?
1. A truck rams into a parked car [Figure 2]
(a) Intuitively, which is larger during the collision: the force exerted by the truck on the car, or the force exerted by the car on the truck?
(b) If you guessed that Newton's 3rd law does not apply to this collision, briefly explain what makes this situation different from when Newton's 3rd law does apply.
2. (Experiment) To simulate this scenario, make the “truck” (a cart with extra weight) crash into the “car” (a regular cart). The truck and car both have force sensors attached. Do whatever experiments you want, to see when Newton's 3rd law applies. Write your results here.
On question 1, most students wrote that the car must feel a larger force, since it reacts more. Therefore, the experimental confirmation of the 3rd law can reinforce students' view that intuitions can't be trusted in physics. To encourage a rethinking of this conclusion, the following questions try to help students see that a certain version of the “car reacts more” intuition is correct and useful.
3. Most people have the intuition that the truck pushes harder on the car than vice versa, because the car “reacts” more strongly during the collision. Let's clarify this reaction intuition to see if we can reconcile it with Newton's 3rd law, which always applies.
(a) Suppose the truck has mass 1000 kg and the car has mass 500 kg. During the collision, suppose the truck loses 5 m/s of speed. Keeping in mind that the car is half as heavy as the truck, how much speed does the car gain during the collision? Visualize the situation, and trust your instincts.
Almost all students answer, correctly, that the car gains twice as much speed as the truck loses. This intuitive idea agrees with Newton's 3rd law, as students find by working through parts (b) through (e):
(b) During the collision, the truck and car push on each other for 0.20 seconds. Find the truck's deceleration during the collision.
(c) Assuming your part (a) intuition is correct, find the car's acceleration during the collision. How does it compare to the truck's acceleration?
(d) Find the net force felt by the truck during the collision. Hint: Use your part (b) answer, and assume friction is negligible.
(e) Assuming your part (a) intuition is correct, find the net force felt by the car during the collision. How does this compare to the force felt by the truck?
Although a small minority of students got lost in the logic and needed some help from the teacher, most students correctly reached the conclusion that, if the car speeds up by twice as much as the truck slows down, then both vehicles must have felt the same force. The subsequent questions emphasize the epistemological importance of this conclusion:
4. Here's the point of question 3: Your own intuition predicts that the car and truck exert equal forces on each other during the collision. But in question 1, many of you said that the truck exerts a larger force on the car than vice versa. So, your intuitions seem to conflict! This is common...
Here, why did your intuitions disagree (if they did)? How can you reconcile your intuitions with each other?
About half the students had no idea how to respond, and many students asked, “What are you looking or here?” The question probably needs to be rewritten. The next question, though very “forcing,” was clear to most students:
5. Here's how I reconcile my conflicting intuitions in this case:
“My intuition says that the car reacts more strongly than the truck reacts during the collision. But by thinking through my intuitions carefully in question 3, I found that my `reaction' intuition is actually an intuition about _____________________, not force.”
Fill in the blank.
Almost all students said “velocity” or “acceleration.” A follow-up discussion may have played a large role in helping students see the pedagogical flow of the lab. I got the sense that, with no follow up, many students would not “get” it.
Questions 4 and 5 invite students to view their “conflicting” intuitions as two different versions of the same basic intuition, the idea that the car reacts more strongly than the truck during the collision. By discovering that one of those two versions is correct and helpful for understanding Newton's 3rd law at an intuitive level, students get a feel for the sense in which the refinement of everyday thinking is part of learning physics.
Class discussion: Refinement of raw intuition
The next day, I led a class discussion designed to underscore this epistemological point. I introduced the distinction between a vague, raw intuition, such as “the car reacts twice as much during the collision,” and a more precise, refined intuition, such as “the car feels twice as large a force during the collision” or “the car has twice as much acceleration during the collision.” In a whole-class discussion punctuated by several small-group discussions and problem-solving interludes, students decided that they possessed the raw “reaction” intuition long before entering physics class. I then pointed out that lab question 1 pushes students to refine that intuition in terms of forces, while question 3 pushes students to refine it in terms of acceleration. Students then traced the implications of those two refinements more fully than they did during the lab. The refinement in terms of acceleration agrees with the intuition that, during the collision, the car speeds up by twice as much as the truck slows down. That refinement not only agrees with, but also helps to explain Newton's 3rd law intuitively: the car reacts more than the truck not because it feels a greater force, but because it's less massive and therefore “reacts” more to the same force. By contrast, the refinement in terms of force disagrees with the 3rd law, and also leads to the counterintuitive conclusion that the car accelerates four times as much as the truck during the conclusion. (Students figured this out in small groups.) Figure 3 shows the state of the whiteboard at the end of this discussion. Again, the main point of this lesson wasn't to rehash the conceptual insights from the lab, but rather, to highlight the epistemological insight that learning physics involves refining rather than selectively ignoring your everyday thinking.
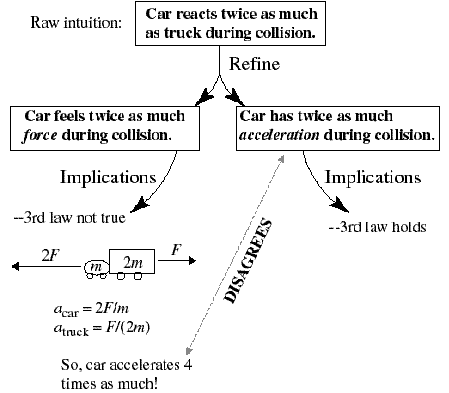
FIGURE 3: Whiteboard at the end of the “refinement” lesson. Students traced the consequences of refining the raw intuition “the car reacts twice as much as the truck” in two different ways. The point was that refining rather than abandoning the raw intuition can help you make sense of Newton's 3rd law. Specifically, the refinement in terms of acceleration highlights the insight that the car “reacts” twice as much as the truck not because it feels more force, but rather, because it's lighter and therefore reacts (accelerates) more in response to the same force.
This subsection traced how I built a particular strand of my epistemological agenda into a connected series of labs, class discussions, and small-group discussions. As compared to materials designed to run themselves with minimal teacher intervention, these materials require the instructor to interacting extensively with students during the labs and to lead substantial class discussions afterwards, especially to help students tie together the epistemological points. Instructors should also assign well-chosen homework problems that reinforce the main conceptual and epistemological points.
I now discuss some other elements of my epistemology-focused curricula.
I regularly assigned homework and in-class problems designed to foster reflection about learning. To encourage honesty (as opposed to “telling the teacher what he wants to hear”), I based grading on the completeness, not the content, of their responses. Sample assignments include:
(a) What role did memorization play in your learning of the material?
(b) What makes the material “hard”?
(c) What advice about how to study would you give to a student taking this course next year?
[In California, asked in October and again in January]
(a) When it comes to helping you learn the material, what are the advantages of putting the textbook-like summaries before the conceptual questions about that same material? Please go into as much detail as possible.
(b) When it comes to helping you learn the material, what are the advantages of putting the textbook-like summaries after the conceptual questions about that same material? Please go into as much detail as possible.
[California and Virginia]
I'm not “yelling” at you or blaming you; I know you're careful, conscientious readers. That's why it's interesting to think about why the apparent contradiction went unnoticed. What could you and/or the textbook have done differently to help you discover—and possibly resolve—the apparent contradiction?
[Virginia]
Students' responses helped me understand their evolving (or non-evolving!) epistemological views throughout the year. For instance, in response to question 1(a), a below-average student answered as follows:
“...In the beginning, I memorized certain types of graphs, thinking they might show up on the test. But this was a really bad idea. I didn't understand the actual concept! Later I realized that I had to understand the concept if I wanted to do well on the quiz....Visualizing a situation or a problem really helps. It really helped me!”
Another average student's response hinted that he was still viewing learning largely as memorization, though focusing on concepts more than formulas:
“While the class is centered around understanding the basic conceptual theories of physics, some memorization is required. Although formulas will be provided, you must know what the formula can solve and why it works. Memorizing the concepts of physics is more important than the formulas...”
A third student put less thought into the question:
“Memorization is not really necessary while doing physics in this class. If you pay attention and ask questions about the things you don't understand you will do well.”
Question 1(c) elicited a full paragraph from most students. I will present results in a separate paper.
In response to the question 3, many students blamed the textbook, without seriously rethinking their reading strategies. It may have helped those students to hear a few of their classmates suggest that thinking of examples and counterexamples—an example of what teachers would call an active learning strategy—might bring apparent contradictions to the surface. In any case, this constant feedback about students' epistemological beliefs helped me plan subsequent classes, and also helped me “nudge” students individually.
My high school and college teaching experiences indicate that many students initially view doing homework as a separate activity from learning and studying. Worried about homework grades, students often copy each others' answers, scour the textbook for a similar problem, and spend disproportionate time on correcting their algebra in order to get the right answer. By contrast, I wanted students to view homework as an opportunity to learn the material, where “learning” involves thinking through a problem, getting feedback, and modifying your thinking accordingly. For this reason, I implemented two untraditional policies.
First, I based students' homework grades entirely on whether their answers showed a good-faith effort to wrestle with the material. Thoughtful wrong answers got higher scores than “rote” correct answers. Grading went just as quickly (or just as slowly!) as traditional grading, depending on how carefully I commented upon students' ideas. This grading system lowered students' anxiety level and removed much of the incentive to “just get through” the homework rather than trying to learn.
Second, I handed out detailed solutions with each assignment, covering some but not all of the assigned questions, so that students could get immediate feedback. You may wonder, “Didn't students just copy your answers?” At first, many of them did. But I gave no credit for answers that were clearly based on mine. More important from an epistemological standpoint, I gave a graded mini-quiz carefully chosen to test conceptual understanding each week for the first five weeks of class. Students who simply copied my homework answers did poorly, and class discussions about this issue helped point them toward why. In addition, students spent much of their in-class time solving problems together in small groups, an experience many of them found helpful for learning the material, as revealed by epistemology homework questions and by class discussions. In brief, the first month of class was explicitly designed to push students toward the epistemological realization that the best way to learn physics is to think through problems, alone and in groups, and then to get feedback; and that acquiring a conceptual understanding is the only way to do well on my quizzes. By the third or fourth mini-quiz, in both California and Virginia, most students had stopped copying my homework solutions. Some students became adept at essentially grading their own homework, with notes to themselves in the margins about insights and mistakes. By the way, students had the opportunity to wipe out their poor mini-quiz scores by demonstrating mastery of the material on a later test.
I don't mean to present too rosy a picture. In California, about 30% of the students often handed in homework that was dashed off with little thought, a “minimal pass,” or didn't hand in homework at all. Interestingly, all but two or three of these students ended up whipping off their own answers instead of copying mine. This didn't indicate epistemological progress. Instead, it reflected the realization that spewing out the first thing that comes to mind is quicker and easier than reading my answer, digesting it, and reproducing it in one's own words (so that I can't tell they copied). With a few exceptions, these students who put minimal effort into homework did poorly on tests. So, my homework policy is no panacea. If a traditionally-graded homework assignments would have elicited more productive effort from this set of students, then my policy harmed their learning. I hypothesize, however, that in a traditionally-graded physics class, these same students would have copied each others' answers or taken other shortcuts around learning. Denying students immediate feedback about some of their homework answers prevents them from copying the teacher's answers, but does not prevent them using other unproductive strategies, such as scouring the textbook for a similar example or searching for the “right” formula.
Among students who were trying to learn the material, either for its own sake or for doing well on tests, the policy generally had the desired effect of focusing students' attention more on learning the concepts and less on getting the right answer. The quality of students' work varied widely; some students put in a lot more thought than others, and many students found the concepts to be very difficult. But even the lower-quality responses generally expressed the students' own ideas.
Trade-offs. Writing the detailed homework solutions takes a lot of time, though you can save hours by handing out previously-published worked problems. [20] Grading all the mini-quizzes takes extra time. Also, especially in California, I had to go extra slowly during the first month, so that students who took a long time to discover productive study strategies had time to catch up.
My homework and tests included many standard quantitative problems. But to reward qualitative, conceptual reasoning—a crucial part of my strategy to push students toward the view that physics knowledge is more conceptual than factual—I asked a high percentage of conceptual questions on homework and tests. Here are some sample test questions (not all from the same test!):
(a) zero
(b) greater than zero, but less than 1000 newtons
(c) equal to 1000 newtons
(d) greater than 1000 newtons
Explain your answer in a few sentences.
[California]
(a) At point C, is the net force on the puck rightward, leftward, or zero? Explain.
(b) Taking rightward as the positive direction, sketch rough graphs of the puck's position, velocity, and acceleration vs. time...
[Virginia]
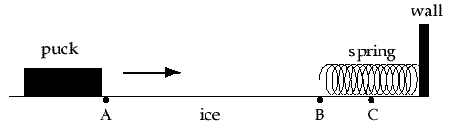
FIGURE 4: Diagram for the puck-and-spring test question, #2. When the puck momentarily comes to rest at point C, is the net force rightward, leftward, or zero?
[California]
(a) Rank the four bulbs in order of brightness. Briefly explain your reasoning, qualitatively (with no calculations).
(b) If bulb 3 burns out (in which case no current flows through it), what happens to the brightness of the other three bulbs? In other words, when 3 burns out, does 1 get brighter or dimmer than it was before? What about bulb 2? What about bulb 4? Briefly explain your reasoning, qualitatively.
[Virginia]
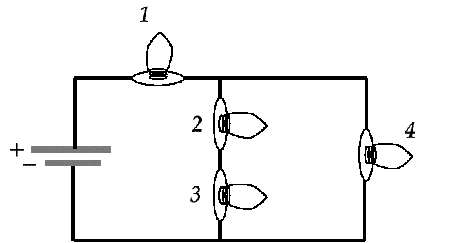
FIGURE 5: Diagram for circuit problem, #4. Students rank the four identical bulbs in order of brightness. Then they consider what happens to the brightness of the remaining bulbs if bulb 3 burns out.
In addition, my quizzes and tests never asked an easy plug `n' chug question. In the past, I included such questions to help weaker students earn points and to help everyone gain confidence. But this well-intentioned policy may have led to an unintended side effect: the reinforcement of students' expectation that rote application of equations leads to success, at least in some cases. Now, when I want to include an easy question, I ask a conceptual question closely and transparently related to an issue students addressed in lab.
The high school textbook I used in California, and the algebra-based college textbook I used in Virginia, cover a huge range of topics, devoting little space to each one. Within a given chapter, the book typically begins by introducing formal definitions and equations, followed by a few examples and real-life applications. By contrast, I was trying to teach students that learning physics often involves starting with real-life examples and common-sense intuitions, and building upon them to make careful definitions, to figure out equations, and so on. During this process, I wanted students to unearth and examine their own intuitive ideas, refining them when needed, an activity the textbook supports only in the most cursory way. So, the textbook and I broadcast conflicting messages about how to learn physics. Although a sophisticated learner can learn from a traditional textbook, a traditional textbook does successfully challenge naïve epistemological beliefs or help students become better learners. For this reason, extensive reliance on the textbook might have undermined my epistemological agenda. I rarely assigned textbook sections other than those introducing factual information.
Since many high school classes make minimal use of textbooks (except perhaps for homework assignments), my neglect of the textbook evoked little response.
Sometimes I deviated from my lesson plan in order to take advantage of a teachable moment. For instance, during a friction lesson in California, the class did an experiment in which a heavy and light book with the same cover are “kicked” across the floor with the same initial speed. They slide the same distance. The ensuing class discussion was intended to help students make sense of this result both intuitively and mathematically. But one student wondered aloud why, when an equally-fast car and truck slam their brakes simultaneously, they slide different distances. Because this question leads to physical and epistemological insight, I made a big deal of it, highlighting the fact that reconciling everyday experience and intuitions with each other and with physics principles is an essential part of learning physics. To reinforce this point, I replaced my planned homework assignment with the student's question about the car vs. truck. (It's a hard question! We discussed it in class the next day.)
I wanted students to understand the difference between a deep understanding and a superficial, rote understanding. To understand this difference, students must actually develop a deep understanding of interconnected chunks of material. Unfortunately, Force Concept Inventory scores and other evidence suggest that, when material is covered at the traditional pace, few students achieve a deep understanding of Newtonian mechanics.12 Because of this, and because discussions of epistemological issues ate up some class and homework time, I slowed down. Especially in California, when students' homework and quizzes indicated a continued lack of understanding, I spent extra time on the topic.
Trade-offs. In California, because students' pace of learning determined the pace of coverage, I covered much less material than originally planned. Judging from their performance on tests containing challenging qualitative problems in addition to standard quantitative problems, most students acquired a basic conceptual understanding of force and motion in one dimension, energy, waves, optics, and aspects of electrostatics. But we skipped momentum, oscillatory motion, electric potential, electric circuits, magnetism, and all of modern physics. Even the leanest reform curricula include some of these topics. Furthermore, because I didn't expose students to interesting topics they couldn't understand deeply, such as particle physics and quantum wave/particle duality, the class was drier than it might have been; my epistemological goals sometimes collided with motivational goals. Specifically, although my California students' average level of agreement with “I am very interested in science” rose from 3.67 out of 5 in September to 4.11 in June (p < 0.05), several students—including some high achievers—remained comparatively uninterested. Some of them might have been turned on by topics I skipped. In addition, my top California students might have learned more breadth, without sacrificing depth, in a faster-paced class.
In Virginia, where I was teaching a pre-established curriculum, I treated many topics (such as oscillatory motion) qualitatively but not quantitatively, and I skipped numerous subtopics covered by the other physics teachers. Those subtopics included much of rotational dynamics, capacitance, and electromagnetic induction. Within a given topic, I often spent more time on the basic concepts at the expense of problem-solving techniques, techniques to which students in other classes were exposed. As a result, my quickest students might have benefited from more coverage.
In the Virginia high school, the physics teachers give a shared midterm and final exam. Because I was skipping and de-emphasizing numerous topics, I was concerned that my students would be ill-prepared. Partly for this reason, throughout the semester I talked with the other teachers to get a detailed sense of the content and difficulty level of the questions they would want to include on the exam. In this way, I tried to figure out the minimum content coverage I could get away with. Then, when it came time to write the midterm and final exam, I took active part, tweaking the exam to be slightly more conceptual and more focused on the core topics than it had been the previous year. As a result, my students were prepared, and performed well. [21] (The other teachers reported being quite happy with the exam, too.) But unless I had monitored the likely contents of the exam, and unless I had taken active part in its formation, my reduction in content coverage could have hurt my students' performance. A poor performance almost certainly would have undermined epistemological messages I was trying to convey.
A paper such as this always invites the criticism that the good results stem not from the explicit curriculum, but from the extra effort, commitment, enthusiasm, or skill of the teacher. Until other instructors implement similar curricular elements, this issue cannot be resolved. In this subsection, however, I argue that the key to success isn't the curriculum or the instructor alone, but rather, a wholehearted commitment to fostering epistemological development manifested in the curriculum and in the instructor's attitude and moment-by-moment actions. If this is correct, then other instructors can have achieve the same results, even though teasing apart instructor effects from curriculum effects becomes less meaningful; where does “curriculum” end and “instructor's real-time decision about what to do next” begin?
Here's the argument. First, the fact that so many excellent physics courses fail to foster significant epistemological change, even courses incorporating some of the curricular elements discussed above, suggests that isolated pieces of epistemologically-focused curriculum aren't enough. Instead, the epistemological focus must suffuse every aspect of the course. Therefore, the instructor's commitment to an epistemological agenda must go beyond a willingness to implement certain curricular elements. For instance, simply replacing a couple of labs with the epistemologically-focused lab/tutorials from section 4.1 may make little difference. I can't stress this enough: we have no reason to think that partial adoption of the curricular elements discussed above will lead to epistemological change.
Second, the classroom atmosphere created by the instructor, and the way she interacts with individual students, undoubtedly plays a large role in fostering reflection about learning. I considered fostering epistemological development to be my primary goal, co-equal with fostering conceptual development about physics. For this reason, I always kept epistemological considerations in the front of my mind when planning lessons, writing materials, setting policies, and interacting with students. In the words of an anonymous reviewer, my implementation of an epistemologically-focused curriculum was holistic and wholehearted. But just this wholeheartedness is an instructor effect doesn't mean other instructors can't be equally wholehearted.
Students' epistemological beliefs—their views about the nature of knowledge and learning—affect their mindset, metacognitive practices, and study habits in a physics course. Even the best reform curricula, however, have not been very successful at helping students develop more sophisticated epistemological beliefs. By contrast, two different epistemologically-focused high-school courses—one honors, one non-honors—led to significant, favorable changes in students' beliefs, as measured by MPEX and by a related assessment. Most of the curricular elements are suitable for both high school and college.
My students, like students in other reform curricula, spent most of their time working in small groups on activities and problems, parts of which resemble tutorials9 and RealTime physics labs.16 But epistemological considerations pervaded every aspect of the course, including homework- and test-question selection, homework-grading policy, class discussions, and even labs. For these reasons, and because a student cannot learn about “understanding” without having the personal experience of understanding chunks of interconnected material, my courses covered fewer concepts and problem-solving techniques than they would have in the absence of an epistemological agenda. Instructors interested in fostering epistemological development must decide if these trade-offs are worth it. This paper aims to spark discussion about these issues, highlighting the possibility of helping students become better learners, while also highlighting the sacrifices entailed by taking this goal seriously.
[1] Edward F. Redish, Richard N. Steinberg, and Jeffery M. Saul, “Student expectations in introductory physics,” Am. J. Phys. 66 (3), 212-224 (1998).
[2] David Hammer, “Epistemological beliefs in introductory physics,” Cognition and Instruction 12 (2), 151-183 (1994). David Hammer, “Two approaches to learning physics,” Phys. Teach. 27 (9), 664-670 (1989).
[3]For instance, see M. Schommer, “The effects of beliefs about the nature of knowledge in comprehension,” J. Ed. Psych. 82 (3), 498 - 504 (1990); Marlene Schommer, Amy Crouse, and Nancy Rhodes, “Epistemological Beliefs and Mathematical Text Comprehension: Believing it is simple does not make it so,” J. Ed. Psych. 84, 435-443 (1992); Nancy B. Songer and Marcia C. Linn, “How do students' views of science influence knowledge integration?,” in Students' models and epistemologies of science, edited by M. C. Linn, N. B. Songer, and E. L. Lewis (1991), Vol. 28, pp. 761-784; Barbara Y. White, “Thinkertools - Causal models, conceptual change, and science education.,” Cognition and Instruction 10 (1), 1-100 (1993).
[4] M. Schommer, “Epistemological Development and Academic Performance Among Secondary Students,” J. Ed. Psych. 85 (3), 406-411 (1993).
[5] Researchers disagree about where to draw the boundaries around epistemology and metacognition. My arguments don't rely on a precise choice of boundary between the two concepts. The following example illustrates the rough boundary I have in mind. Suppose a student, after reading a paragraph of her textbook, rephrases the material in her own words. This is a metacognitive practice. But the practice might be driven, in part, by the epistemological outlook that “knowing” involves constructing one's own understanding as opposed to just absorbing information.
[6] At a bigger high school, many of my students might have opted for an “honors” physics class or a “conceptual” (low-math) physics class.
[7] See http://www.physics.umd.edu/rgroups/ripe/perg/expects/mpex.htm for the full survey.
[8] Barbara White, Andrew Elby, John Frederiksen, and Christina Schwarz, “The Epistemological Beliefs Assessment for Physical Science,” presented at the American Education Research Association, Montreal, 1999 (unpublished).
[9] Lillian C. McDermott, Peter S. Shaffer, and the Physics Education Group, Tutorials in Introductory Physics, Preliminary edition ed. (Prentice Hall, Upper Saddle River, NJ, 1998). For discussion, see Lillian C. McDermott and Peter S. Shaffer, “Research as a guide for curriculum development: An example from introductory electricity. Part I: Investigation of student understanding.,” Am. J. Phys. 60 (11), 994-1003 (1992).
[10] Patricia Heller, Ron Keith, and S. Anderson, “Teaching problem solving through cooperative grouping. Part 1: Group vs. individual problem solving,” Am. J. Phys. 60 (7), 627-636 (1992)
Patricia Heller and Mark Hollabaugh, “Teaching problem solving through cooperative grouping. Part 1: Group versus individual problem solving,” Am. J. Phys. 60 (7), 637-644 (1992).
[11] Priscilla Laws, “Workshop physics: replacing lectures with real experience,” in Computers in Physics Instruction: Proceedings, edited by E. F. Redish. and J. S. Riley (Addison-Wesley, Reading, MA, 1989); Priscilla W. Laws, “Calculus-based physics without lectures,” Physics Today 44 (12), 24-31 (1991); P. W. Laws, “New approaches to science and mathematics teaching at liberal arts colleges,” Daedalus 128 (1), 217-240 (1999).
[12] Richard R. Hake, “Interactive-engagement vs. traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses,” Am. J. Phys. 66 (1), 64-74 (1998).
[13] To get a sense of the correspondence, we can calculate the correlation coefficient between students' scores on an EBAPS subscale and their scores on the corresponding MPEX cluster. The correlation between EBAPS Structure of Knowledge and the sum of MPEX Concepts and Coherence is .65. The correlation between EBAPS Nature of Learning and MPEX Independence is .42. Those correlations are both statistically significant to p < .05. By contrast, the correlation between EBAPS Real-life applicability and MPEX Reality link is only .23, which is of marginal statistical significance (p = .09). The low correlation reflects a substantive difference between the two subscales. MPEX Reality link focuses partly on students' views about whether they will use physics concepts outside the classroom, whereas EBAPS focuses more on students views about whether, in principle, classroom physics concepts describe phenomena in the real world.
[14] Marlene Schommer, Amy Crouse, and Nancy Rhodes, “Epistemological Beliefs and Mathematical Text Comprehension: Believing it is simple does not make it so,” J. Ed. Psych. 84, 435-443 (1992).
[15] After we finished Newtonian mechanics, my students achieved an average score of 84% on the Force Concept Inventory, comparable to the post-test scores of Harvard students; see Hake.12 I did not give my students the FCI as a pre-test. An independent sample of 250 other 11th grade physics students at the same school took the FCI as a pre-test, achieving an average score of 32%. My California students did not take the FCI, but generally performed well on FCI-like questions included on tests, including those presented in section 4.4.
[16] David R. Sokoloff, Ronald K. Thornton, and Priscilla W. Laws, RealTime physics : active learning laboratories (Wiley, New York, 1999). For discussion, see Ronald Thornton and David Sokoloff, “Learning motion concepts using real-time microcomputer-based laboratory tools,” Am. J. Phys. 58 (9), 858-66 (1990).
[17] See Eric Mazur, Peer instruction: a user's manual (Prentice Hall, Upper Saddle River, NJ, 1997).
[18] “The whole of science is nothing more than a refinement of everyday thinking. It is for this reason that the critical thinking of the physicist cannot possibly be restricted to the examination of concepts
from his own specific field. He cannot proceed without considering critically a much more difficult problem, the problem of analyzing the nature of everyday thinking.” -- Albert Einstein, “Physics and Reality,” J. of the Franklin Institute 221 (1936).
[19] David Hammer, “Students' beliefs about conceptual knowledge in introductory physics,” International Journal of Science Education 16 (4), 385-403 (1994).
[20] Many textbooks come with an instructor's solution manual or a study guide with worked problems. Other sources of problems with detailed solutions include Andrew Elby, The Portable T.A.: a physics problem solving guide. (Prentice-Hall, Upper Saddle River, NJ, 1998); and Research and Education Association and M. Fogiel, The physics problem solver (Rea, New York, 1976).
[21]On the multiple-choice section, consisting mostly of difficult conceptual questions, my students outperformed the school average by a statistically significant amount. Since each teacher graded his or her own students' free-response questions, such comparisons are not possible for those items.